Unique Wave-Window Combinations

2007-12-17

The previous page lays out ALL POSSIBLE combinations of waves and windows. This is a very thorough approach, and at the time I didn't know if I would find unexpected differences. But the results turned out to be very consistent, and therefore included a lot of redundancies.

This page restates in a single table all of the UNIQUE combinations of waves. In other words, I took all 512 possible combinations and eliminated everything redundant. I think it's nice to see all the possibilities on one page with no redundancies.

Test Procedure

The thing I need to explain here is how I figured out which wave and window combinations are UNIQUE. First, I started with a logic table showing all of the unique wave combinations:

000-000	000-001	000-010	000-011	000-100	000-101	000-110	000-111
001-000	001-001	001-010	001-011	001-100	001-101	001-110	001-111
010-000	010-001	010-010	010-011	010-100	010-101	010-110	010-111
011-000	011-001	011-010	011-011	011-100	011-101	011-110	011-111
100-000	100-001	100-010	100-011	100-100	100-101	100-110	100-111
101-000	101-001	101-010	101-011	101-100	101-101	101-110	101-111
110-000	110-001	110-010	110-011	110-100	110-101	110-110	110-111
111-000	111-001	111-010	111-011	111-100	111-101	111-110	111-111

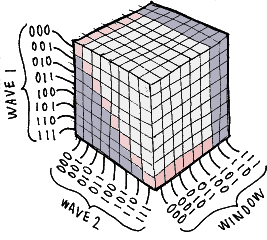
"Logic Cube" showing the 512 possibilities,
216 of which are unique

The white squares are unique combinations, the pink squares are valid but are more easily achieved by using a single wave, and the blue squares are not unique because they are just reversed versions of waves already shown in white.

If you count them, there are 36 white and pink squares. You can run those 36 unique wave combinations through 6 unique window functions for a total of 216 unique wave and window combinations (36 x 6 = 216).

I made the illustration at right to show that if you take the logic table above and extrude it into three dimensions, you have a "logic cube" that shows all the possibilities.

There are 8 choices for WAVE 1, 8 choices for WAVE 2, and 8 choices for WINDOW. The 512 resulting possibilities are shown as an 8 x 8 x 8 cube.

Notice the front of the cube looks just like the logic table. Then it is extruded back to account for the 8 kinds of window function. Note that Window 110 and Window 111 are shaded, because they are the same as Window 101.

Unique Wave-Window Combinations Demo

The next step is to show each of the 216 unique combinations in one table, and provide audio samples for everything in the table.

The table starts off with the 8 basic waveforms, and then goes on to the unique combinations of waves. Anything that would cause a repetition is thrown out.

216 unique wave-window combinations
Click table for full-size image

Key for this table

: This option is available through the front panel.
: This option is only available through sysex.

Audio Files

These audio files accompany the table above. Each audio file represents one row of the table. Each audio file takes a unique wave-window combination and passes it through the 8 window functions. The 7th and 8th window functions are repeats of the 6th, so act like you didn't hear those.

Summary

It should be obvious that there are a lot more than 33 possiblities when using sysex. I think that a lot of these possibilities are not just junk, some are usable.

11809.74600